前言
本文为算法分析系列博文之一,深入探究桶排序,分析各自环境下的性能,同时辅以性能分析示例加以佐证
实现思路与步骤
思路
- 设置固定空桶数
- 将数据放到对应的空桶中
- 将每个不为空的桶进行排序
- 拼接不为空的桶中的数据,得到结果
步骤演示
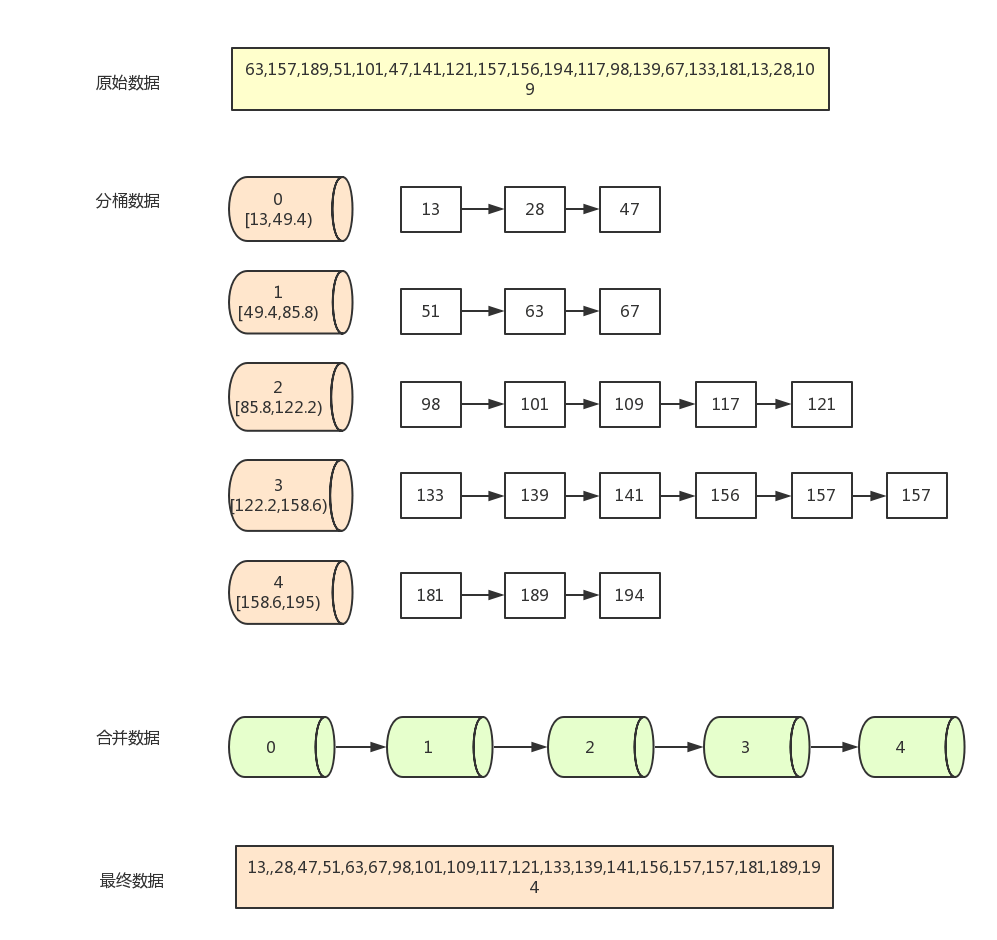
假设一组数据(20长度)为
[63,157,189,51,101,47,141,121,157,156,194,117,98,139,67,133,181,13,28,109]
现在需要按5个分桶,进行桶排序,实现步骤如下:
-
找到数组中的最大值194和最小值13,然后根据桶数为5,计算出每个桶中的数据范围为
(194-13+1)/5=36.4 - 遍历原始数据,(以第一个数据63为例)先找到该数据对应的桶序列
Math.floor(63 - 13) / 36.4) =1,然后将该数据放入序列为1的桶中(从0开始算) - 当向同一个序列的桶中第二次插入数据时,判断桶中已存在的数字与新插入的数字的大小,按从左到右,从小打大的顺序插入。如第一个桶已经有了63,再插入51,67后,桶中的排序为(51,63,67) 一般通过链表来存放桶中数据,但js中可以使用数组来模拟
- 全部数据装桶完毕后,按序列,从小到大合并所有非空的桶(如0,1,2,3,4桶)
- 合并完之后就是已经排完序的数据
步骤图示
实现代码
以下分别以JS和Java的实现代码为例
JS实现代码(数组替代链表版本)
var bucketSort = function(arr, bucketCount) {
if (arr.length <= 1) {
return arr;
}
bucketCount = bucketCount || 10;
//初始化桶
var len = arr.length,
buckets = [],
result = [],
max = arr[0],
min = arr[0];
for (var i = 1; i < len; i++) {
min = min <= arr[i] ? min: arr[i];
max = max >= arr[i] ? max: arr[i];
}
//求出每一个桶的数值范围
var space = (max - min + 1) / bucketCount;
//将数值装入桶中
for (var i = 0; i < len; i++) {
//找到相应的桶序列
var index = Math.floor((arr[i] - min) / space);
//判断是否桶中已经有数值
if (buckets[index]) {
//数组从小到大排列
var bucket = buckets[index];
var k = bucket.length - 1;
while (k >= 0 && buckets[index][k] > arr[i]) {
buckets[index][k + 1] = buckets[index][k];
k--
}
buckets[index][k + 1] = arr[i];
} else {
//新增数值入桶,暂时用数组模拟链表
buckets[index] = [];
buckets[index].push(arr[i]);
}
}
//开始合并数组
var n = 0;
while (n < bucketCount) {
if (buckets[n]) {
result = result.concat(buckets[n]);
}
n++;
}
return result;
};
//开始排序
arr = bucketSort(arr, self.bucketCount);
JS实现代码(模拟链表实现版本)
var L = require('linklist'); //链表
var sort = function(arr, bucketCount) {
if(arr.length <= 1) {
return arr;
}
bucketCount = bucketCount || 10;
//初始化桶
var len = arr.length,
buckets = [],
result = [],
max = arr[0],
min = arr[0];
for(var i = 1; i < len; i++) {
min = min <= arr[i] ? min : arr[i];
max = max >= arr[i] ? max : arr[i];
}
//求出每一个桶的数值范围
var space = (max - min + 1) / bucketCount;
//将数值装入桶中
for(var i = 0; i < len; i++) {
//找到相应的桶序列
var index = Math.floor((arr[i] - min) / space);
//判断是否桶中已经有数值
if(buckets[index]) {
//数组从小到大排列
var bucket = buckets[index];
var insert = false; //插入标石
L.reTraversal(bucket, function(item, done) {
if(arr[i] <= item.v) { //小于,左边插入
L.append(item, _val(arr[i]));
insert = true;
done(); //退出遍历
}
});
if(!insert) { //大于,右边插入
L.append(bucket, _val(arr[i]));
}
} else {
var bucket = L.init();
L.append(bucket, _val(arr[i]));
buckets[index] = bucket; //链表实现
}
}
//开始合并数组
for(var i = 0, j = 0; i < bucketCount; i++) {
L.reTraversal(buckets[i], function(item) {
// console.log(i+":"+item.v);
result[j++] = item.v;
});
}
return result;
};
//链表存储对象
function _val(v) {
return {
v: v
}
}
//开始排序
arr = bucketSort(arr, self.bucketCount);
其中,linklist为引用的第三方库,地址 linklist
Java实现代码
public static double[] bucketSort(double arr[], int bucketCount) {
int len = arr.length;
double[] result = new double[len];
double min = arr[0];
double max = arr[0];
//找到最大值和最小值
for (int i = 1; i < len; i++) {
min = min <= arr[i] ? min: arr[i];
max = max >= arr[i] ? max: arr[i];
}
//求出每一个桶的数值范围
double space = (max - min + 1) / bucketCount;
//先创建好每一个桶的空间,这里使用了泛型数组
ArrayList < Double > [] arrList = new ArrayList[bucketCount];
//把arr中的数均匀的的分布到[0,1)上,每个桶是一个list,存放落在此桶上的元素
for (int i = 0; i < len; i++) {
int index = (int) Math.floor((arr[i] - min) / space);
if (arrList[index] == null) {
//如果链表里没有东西
arrList[index] = new ArrayList < Double > ();
arrList[index].add(arr[i]);
} else {
//排序
int k = arrList[index].size() - 1;
while (k >= 0 && (Double) arrList[index].get(k) > arr[i]) {
if (k + 1 > arrList[index].size() - 1) {
arrList[index].add(arrList[index].get(k));
} else {
arrList[index].set(k + 1, arrList[index].get(k));
}
k--;
}
if (k + 1 > arrList[index].size() - 1) {
arrList[index].add(arr[i]);
} else {
arrList[index].set(k + 1, arr[i]);
}
}
}
//把各个桶的排序结果合并 ,count是当前的数组下标
int count = 0;
for (int i = 0; i < bucketCount; i++) {
if (null != arrList[i] && arrList[i].size() > 0) {
Iterator < Double > iter = arrList[i].iterator();
while (iter.hasNext()) {
Double d = (Double) iter.next();
result[count] = d;
count++;
}
}
}
return result;
}
//开始排序,其中arr为需要排序的数组
double[] result = bucketSort(arr,bucketCount);
算法复杂度
算法复杂度的计算,这里我们直接抛开常数,只计算与N(数组长度)与M(分桶数)相关的语句
时间复杂度
因为时间复杂度度考虑的是最坏的情况,所以桶排序的时间复杂度可以这样去看(只看主要耗时部分,而且常熟部分K一般都省去)
- N次循环,每一个数据装入桶
- 然后M次循环,每一个桶中的数据进行排序(每一个桶中有N/M个数据),假设为使用比较先进的排序算法进行排序
一般较为先进的排序算法时间复杂度是O(N*logN),实际的桶排序执行过程中,桶中数据是以链表形式插入的,那么整个桶排序的时间复杂度为:
O(N)+O(M*(N/M)*log(N/M))=O(N*(log(N/M)+1))
所以,理论上来说(N个数都符合均匀分布),当M=N时,有一个最小值为O(N)
PS:这里有人提到最后还有M个桶的合并,其实首先M一般远小于N,其次再效率最高时是M=N,这是就算把这个算进去,也是O(N(1+log(N/M)+M/N)),极小值还是O(2N)=O(N)
求M的极小值,具体计算为:(其中N可以看作一个很大的常数)
F(M) = log(N/M)+M/N) = LogN-LogM+M/N
它的导函数
F'(M) = -1/M + 1/N
因为导函数大于0代表函数递增,小于0代表函数递减
所以F(M)在(0,N) 上递减
在(N,+∞)上递增
所以当M=N时取到极小值
空间复杂度
空间复杂度一般指算法执行过程中需要的额外存储空间
桶排序中,需要创建M个桶的额外空间,以及N个元素的额外空间
所以桶排序的空间复杂度为 O(N+M)
稳定性
稳定性是指,比如a在b前面,a=b,排序后,a仍然应该在b前面,这样就算稳定的。
桶排序中,假如升序排列,a已经在桶中,b插进来是永远都会a右边的(因为一般是从右到左,如果不小于当前元素,则插入改元素的右侧)
所以桶排序是稳定的
PS:当然了,如果采用元素插入后再分别进行桶内排序,并且桶内排序算法采用快速排序,那么就不是稳定的
适用范围
用排序主要适用于均匀分布的数字数组,在这种情况下能够达到最大效率
性能分析
为了更好的测试桶排序在各自环境的性能,分别用普通JS浏览器,Node.js环境,Java环境进行测试,得出以下的对比分析
前提数据为:
- 10W长度的随机数组
- 数组的范围为[0,10000)
- 数据为浮点类型
JS浏览器环境下的性能(数组替代链表型)
本文主要是在webkit内核的浏览器中测试,浏览器中的方案类型为
- 数据插入时排序,但是使用数组替代链表
出人意料,答案并非是理想的那样。
结果为:
- 当分桶数从1-500时,排序效率有所提升(其中[1,100]提升的比较明显)
- 当分桶数大于500后,再增加分桶数,性能反而会有明显下降
- 而且,排序时间过长,已经超过了毫秒级别
- 所以,明显并不符合理想预期
详细结果
以下为在前提条件下,分桶数从10-10000变化的耗时对比
| 分桶数 | 耗时 | 趋势 |
|---|---|---|
| 10 | 24444ms | 递减 |
| 100 | 3246ms | 递减 |
| 500 | 3104ms | 递减 |
| 1000 | 3482ms | 递增 |
| 10000 | 9185ms | 递增 |
图示
其中,分桶为500时的一个排序结果图示(其中平均排序时间在2-3S,超过了理想模型下的预期时间)

为了探讨是桶排序自身的原因还是JS浏览器环境的局限,所以又单独在Node.js环境下和Java环境下进行分析测试
Node.js环境下的性能(数组替代链表型)
这种方案下采用和浏览器中一样的代码(数组替代链表型)
结果为:
- 当分桶数从1-500时,排序效率有所提升(其中[1,100]提升的比较明显)
- 当分桶数大于500后,再增加分桶数,性能反而会有明显下降
- 而且,排序时间过长,已经超过了毫秒级别
- 所以,明显并不符合理想预期模型
详细结果
以下为在前提条件下,分桶数从1-1000000变化的耗时对比
| 分桶数 | 耗时 | 趋势 |
|---|---|---|
| 1 | 9964ms | 递减 |
| 10 | 1814ms | 递减 |
| 100 | 279ms | 递减 |
| 500 | 204ms | 递减 |
| 1000 | 262ms | 递增 |
| 5000 | 1078ms | 递增 |
| 10000 | 2171ms | 递增 |
| 100000 | 9110ms | 递增 |
Node.js环境下的性能(模拟链表型)
这种方案下采用和浏览器中一样的代码(模拟链表型),这种方案里的主要差别是不再使用数组替代链表,而是采用模拟链表的方式
结果为:
- 整个1-100000区间,随着分桶数的增加,效率是递增的
- 当分桶数从1-1000时,性能远远小于前面的那种数组替代链表类型
- 当分桶数大于1000后,再增加分桶数,性能才逐渐超过前面的那种类型
- 所以,虽然说这种算法在分桶数较低时性能很低,但是当分桶数提高时,性能有着明显的提供,而且性能和分桶数是线性关系,符合理想预期模型
详细结果
以下为在前提条件下,分桶数从1-1000000变化的耗时对比
| 分桶数 | 耗时 | 趋势 |
|---|---|---|
| 1 | 196405ms | 递减 |
| 10 | 30527ms | 递减 |
| 100 | 3029ms | 递减 |
| 500 | 976ms | 递减 |
| 1000 | 643ms | 递减 |
| 5000 | 340ms | 递减 |
| 10000 | 276ms | 递减 |
| 100000 | 312ms | 稳定 |
| 1000000 | 765ms | 递增 |
Java环境下的性能
这种方案主要用来和Node.js后台执行方案的对比
结果为:
- 分桶数从小到大增加时,性能逐步增加
- 当分桶数在10000左右时,达到性能最大值
- 分桶数在往后增加也不会影响性能(因为实际上没有用到计算)
- 虽然说与理想值还有一点差距,但整个结果基本符合预期
详细结果
以下为在前提条件下,分桶数从1-1000000变化的耗时对比
| 分桶数 | 耗时 | 趋势 |
|---|---|---|
| 1 | 39610ms | 递减 |
| 10 | 6094ms | 递减 |
| 100 | 1127ms | 递减 |
| 500 | 361ms | 递减 |
| 10000 | 192ms | 递减 |
| 100000 | 195ms | 稳定 |
| 1000000 | 198ms | 稳定 |
总结
桶排序决定快慢的关键在于桶内元素的排序算法,所以不同的实现算法,相应的排序代价也是不一样的
比如,本文中的几个对比
- 使用数组模拟链表,桶内元素插入时即排序
- 使用模拟链表,桶内元素插入时即排序
以上几种的排序方案,最终的结果都是不一样的。 而且还有一点值得注意,浏览器中执行的性能损耗要远大于后端执行。
关于JS数组替代链表方案的性能疑惑
最开始分析桶排序时,只采用了JS数组替代链表的方案,那时候发现当分桶数大于一定阈值时,性能会有一个明显的下降,刚开始还比较疑惑,不知道是桶排序自身的问题还是浏览器环境的限制还是算法的问题。
直到后来又分别在Java环境,Node.js环境进行测试,并且尝试更换算法,最终发现原来有以下原因:
- 浏览器中执行的性能损耗要远大于后端执行
- 使用数组替代链表型,这个方案本身有问题
- 另外还试过使用数组替代链表,先插入数据,全部插入完毕后再单个桶内进行快速排序,结果表明这种方案的结果与前面的数组替代链表型是基本一致的
而且后来采用模拟链表方案,发现结果确实是与预期预估的趋势相符合的。
所以基本锁定的原因就是:JS中使用数组替代链表这种方案本身就不合理
关于如何选择桶排序方案
上述分析中可以看到,当分桶数较小时,模拟链表方案性能要远远小于数组替代链表方案,但基本上当分桶数大于1000多时,模拟链表方案的优势就体现出来了。 所以实际情况可以根据实际的需要进行选择
示例Demo
仍然和以前的系列一样,有提供一个浏览器环境下的性能分析示例工具,参考 JS几种数组排序方式分析比较
原文地址
原文在我个人博客上面 排序算法之桶排序的深入理解以及性能分析